Traversing in Data Structure: A Complete Guide

Introduction

Data structures are the backbone of programming. They allow us to store, organize, and manage data efficiently. But storing data is just one part of the puzzle. To make the data useful, we need to traverse it. Traversing in data structure means visiting each element in a systematic way. It’s like reading a book from start to finish or checking each item in a grocery list. Without proper traversal, even the most well-organized data structure can become useless. In this article, we’ll explore everything you need to know about traversing, with simple explanations, real examples, and practical tips.

What Is Traversing in Data Structure?

Traversing is the process of accessing every element in a data structure at least once. Whether the structure is simple like an array or complex like a tree, traversing ensures you can read, update, or manipulate data efficiently. Think of a data structure as a neighborhood. Traversing is like visiting every house to check who lives there or deliver a message. Traversal is fundamental because without it, operations like searching, sorting, and updating would be impossible.

Why Traversing Is Important

Traversal is crucial for several reasons:

1. Data Access – Without traversing, you cannot read or use data effectively.
2. Data Manipulation – Traversing allows adding, deleting, or updating elements.
3. Algorithm Implementation – Many algorithms, like searching or sorting, rely on traversal.
4. Data Analysis – Traversing enables operations like finding sums, averages, or maximum values.

Imagine a database of students. If you want to find the top scorer, you must traverse the list. Traversing makes data meaningful and actionable.

Types of Data Structures

To understand traversal better, you must know the types of data structures:

1. Linear Data Structures – Data elements are arranged sequentially. Examples: arrays, linked lists, stacks, queues.
2. Non-linear Data Structures – Data elements are connected in a hierarchical or networked way. Examples: trees, graphs.

Traversal methods depend on the type of structure. Linear structures are easier to traverse, while non-linear structures may require more complex strategies.

Traversal in Linear Data Structures

Linear data structures are the simplest to traverse because their elements are arranged in order. Common methods include:

1. Array Traversal – Use a loop to visit each element. For example, for(int i=0; i<n; i++).
2. Linked List Traversal – Start at the head node and move to the next until you reach the end.

Linear traversal is straightforward and forms the basis for more complex traversal techniques in non-linear structures.

Traversal in Non-linear Data Structures

Non-linear structures like trees and graphs need special traversal strategies. These structures don’t have a fixed sequence, so traversal must follow certain rules.

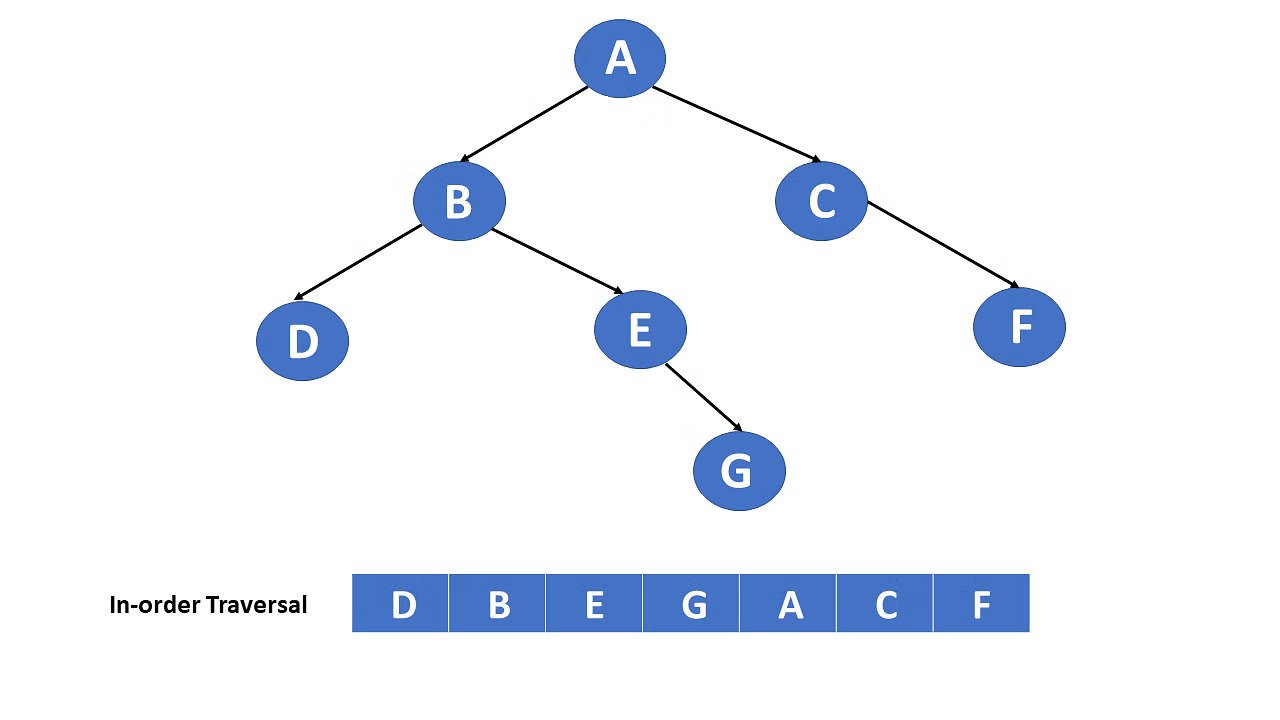
• Tree Traversal – Methods include preorder, inorder, and postorder. Each method visits nodes in a different order, depending on the use case.
• Graph Traversal – Common methods are Depth-First Search (DFS) and Breadth-First Search (BFS). These help in finding paths, shortest routes, or connectivity between nodes.

Non-linear traversal can be tricky, but understanding it is essential for tasks like database searches, AI, or networking.

Preorder, Inorder, and Postorder Traversal in Trees

Tree traversal has three main types:

1. Preorder – Visit root → left → right. Useful for copying trees.
2. Inorder – Visit left → root → right. Useful for sorted data retrieval.
3. Postorder – Visit left → right → root. Useful for deleting a tree.

For example, consider a family tree. Preorder lets you see the parent before the children, while postorder lets you see children before the parent. Understanding these helps in problem-solving.

Depth-First Search (DFS) in Graphs

DFS is a graph traversal method where we explore as far as possible along a branch before backtracking. It’s like exploring a maze by taking one path fully before trying another. DFS can be implemented using a stack or recursion. It’s useful for:

• Detecting cycles in graphs
• Finding connected components
• Solving puzzles and games

DFS is powerful but can consume memory if the graph is huge, so careful implementation is essential.

Breadth-First Search (BFS) in Graphs

BFS is another graph traversal method. It explores all neighbors at the current level before moving deeper. Think of BFS like a wave spreading from a starting point. BFS is often implemented using a queue. It’s especially useful for:

• Finding the shortest path in unweighted graphs
• Level-order traversal of trees
• Social network analysis

BFS complements DFS and is chosen depending on the problem requirements.

Recursive vs Iterative Traversal

Traversal can be performed in two ways:

1. Recursive Traversal – The function calls itself to visit nodes. It’s simple to write but can cause stack overflow for large data.
2. Iterative Traversal – Uses loops and auxiliary structures like stacks or queues. It’s more memory-efficient and avoids deep recursion issues.

For example, a linked list can be traversed recursively or iteratively, and both achieve the same result. Choosing the right method depends on memory limits and problem complexity.

Common Traversal Mistakes and How to Avoid Them

While traversing seems simple, beginners often make mistakes:

• Forgetting the stopping condition, causing infinite loops
• Ignoring edge cases like empty lists or null nodes
• Using recursion without considering memory limitations

The best approach is to plan your traversal carefully. Test on small examples first, then scale up. Writing pseudocode before implementation also reduces errors.

Real-Life Applications of Traversal

Traversal isn’t just theoretical. It’s everywhere in programming and technology:

• File Systems – Traversing folders to list files
• Web Crawlers – Traversing websites to index content
• Social Networks – Traversing friends and followers
• Games – Traversing maps or AI decision trees

Understanding traversal deeply makes you a better problem solver and programmer.

Optimizing Traversal for Efficiency

Traversal can become slow for large data structures. Here’s how to optimize:

• Use the right traversal method for the data structure
• Avoid redundant visits using visited flags or hash sets
• Choose iterative over recursive for large structures to save stack space
• Minimize operations inside the traversal loop

Efficient traversal saves time and resources, which is crucial for real-world applications.

FAQs About Traversing in Data Structure

1. What is the main purpose of traversing in data structures?
Traversing ensures that every element in a data structure is accessed at least once. It helps in searching, updating, or analyzing data efficiently.

2. Which traversal is best for arrays?
Arrays are linear structures. Simple for-loops or while-loops are most efficient for traversing arrays.

3. How is DFS different from BFS?
DFS explores as deep as possible before backtracking. BFS explores all neighbors level by level.

4. Can traversal be done recursively?
Yes, traversal can be recursive. It’s simple but can cause stack overflow if the structure is very large.

5. Why is traversal important in trees?
Traversal in trees is crucial for tasks like searching, sorting, printing, and deleting nodes.

6. Can traversal improve algorithm performance?
Yes. Efficient traversal reduces unnecessary operations, improving speed and memory usage in algorithms.

Conclusion

Traversing in data structure is more than just visiting elements it’s the gateway to understanding, manipulating, and extracting value from data. From arrays to graphs, knowing how to traverse efficiently is a must for any programmer. By mastering traversal, you unlock the power of algorithms, optimize performance, and solve real-world problems with confidence. Start practicing different traversal methods today, and see how much easier complex data handling becomes.